المشروع 4 – الأشكال الهندسية

الهدف من هذا المشروع هو أن نبين لك كيف يمكنك رسم بعض الأشكال الهندسية المنتظمة أي تكون جميع أضلاعها متساوية و كذلك زواياها متساوية في القياس.

القاعدة الأولى لرسم الأشكال المبيّنة في الصورة التالية، أن يدور القلم دورة تساوي °360.

لكي نرسم هذه الأشكال نستعمل اللبنات من زمرة الحركة: تحرك و استدر.

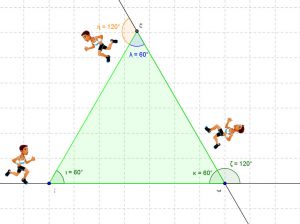
نأخذ مثال المثلث، أنظر إلى الصورة. للمثلث ثلاث أضلاع و ثلاث زوايا. نفرض أن لاعب ما، يجري ليرسم مثلث متساوي الأضلاع:

triangle_opt

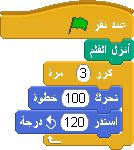
المقطع البرمجي إذن يكون:

triangle-code_opt

فلننظر حالة خماسي الأضلاع كما في الصورة التالية.

الشكل الخماسي له 5 أضلاع و 5 زوايا. تبين لك الأسهم جهة الحركة لرسم الشكل.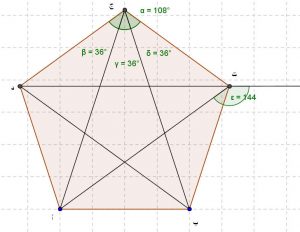 star_opt

يقوم الكائن بالتحرك مسافة محددة ثم يدور بزاوية:

°180 – °108 = °72.

لرسم الشكل الخماسي ننشئ البرنامج التالي.

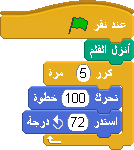
pentagon-script_opt

من المثالين السابقين نستنتج مايلي:

عدد تكرار الحلقات يساوي عدد الزوايا الداخلية للشكل.

زاوية الدوران تساوي °180 (زاوية مسطحة) ناقص الزاوية الداخلية.

الجدول التالي يلخص زوايا قمم بعض أشكال متعددة الأضلاع.

تتكون النجمة من خمسة قمم و يمكن رسمها داخل شكل خماسي كما هو موضح في الصورة التالية.

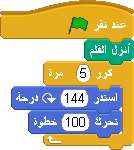
إذا كان الكائن متواجد في النقطة ت، فإنه يتعين عليه الدوران بزاوية تساوي °144. لاحظ كيف يعمل المقطع التالي.

حاول إنشاء الأشكال التالية و غيرها إستناداً لما تعلمته في هذا المشروع.

pen-formes-fw_opt

إلكترونيات